Search
Compare Products

LoPro® Robot Transfer Units

main product photo
New
Be the first to review this product

Both traditional and collaborative robots can benefit from Bishop-Wisecarver 7th Axis Robot Transfer Units. LoPro® RTU-L and LoPro® RTU-M are available for light and medium capacity applications. Each system is designed for durability, ease of installation, and low total cost of ownership. Our expert application engineers can help you select the complete 7th axis system solution that is right for you, or customize a solution to meet your exact requirements.

Chat with us to learn more about this product.
SKU
lopro-rtu
Wish List Compare
  •  Request a Quote
    • Related Products
    Check items to add to the cart or
Technical Specification

Stock Codes

LoPro RTU stock code system

System Capabilities

 

Vertical Force
(LA)

Horizontal Force
(LR)

Vertical Moment
(MY)

Horizontal Moment
(MR)

Horizontal Moment
(MP)

Thrust
(Approximate, Slow Speed)
  N N N-m N-m N-m N

LoPro RTU-L
(Light Capacity, Single Wheel Plate)

 15684 19012 1478 1174 1220 2818

LoPro RTU-M
(Medium Capacity,  Double Wheel Plate)

 31368 38024 2956 2348 2440 2818

 

 

Load & Life Calculation

<!-----------STYLE---------------> <style> .math-box { font-family: Cambria, Georgia, serif; font-size: 22px; font-weight: bold; } .math-box .fract-box { display: inline-block; text-align: center; position: relative; top: 18px; } .math-box .fract-bar { border-bottom-style: solid; border-bottom-width: 1px; } </style>

The following equation is for the purpose of estimating the applied load factor to the wheel plate and track plate only. System drive components are not accounted for, but should also be considered. The expected life of the system (in travel length, such as inches or kilometers) is calculated using:

<div class="math-box"><!------start of math div---------> Life = <div class="fract-box"><span style="font-style: italic;">L<sub>C</sub></span> <div class="fract-bar"></div> (<span style="font-style: italic;">L<sub>F</sub></span>)<sup>3</sup></div> *<span style="font-style: italic;">A<sub>F</sub></span></div> <!-----end of math div------>

 

 

The Life Constant (Lc) is given in the table on the right.

The Adjustment Factor (Lf) is estimated based on the severity of application conditions (see table on the right).

The Load Factor (Lf) is calculated using the application's applied forces/moments and force/moment capacities of the system as follows:

<div class="math-box"><!------start of math div---------> <span style="font-style: italic;"> L<sub>f</sub> </span> = <div class="fract-box"><span style="font-style: italic;">F<sub>vertical</sub></span> <div class="fract-bar"></div> <span style="font-style: italic;">L<sub>A(max)</sub></span></div> + <div class="fract-box"><span style="font-style: italic;">F<sub>horizontal</sub></span> <div class="fract-bar"></div> <span style="font-style: italic;">L<sub>R(max)</sub></span></div> + <div class="fract-box"><span style="font-style: italic;">M<sub>vertical</sub></span> <div class="fract-bar"></div> <span style="font-style: italic;">M<sub>Y(max)</sub></span></div> + <div class="fract-box"><span style="font-style: italic;">M<sub>horizontal</sub></span> <div class="fract-bar"></div> <span style="font-style: italic;">M<sub>R(max)</sub></span></div> </div> <!-----end of math div------>

 

 

Refer to the illustration on the right for directions of each component. Any forces applied on the wheel plate need to be considered, including inertial forces, gravitational forces, external forces such as tool pressure, impact loading, and payload.

The most conservative calculations will use max foundational loading values from robot manufacturer catalogs. Note that since the robot can only be extended in one horizontal direction, pitch moment (MP) found in other LoPro actuator-based system calculations is ignored.

If assistance is required in resolving specific loads into the resultant forces, please contact our Applications Engineering staff.

 

 

 

 

load orientation diagram

 

life constant and adjustment factor charts

Enter the necessary mounting capacities of your robot, or select an example robot from the list below:

<!---------FORCE INPUTS------------> <table> <tbody> <tr> <td>Vertical Force (N):</td> <td><input id="input_la" tabindex="0" type="number"></td> </tr> <tr> <td>Horizontal Force (N):</td> <td><input id="input_lr" tabindex="0" type="number"></td> </tr> <tr> <td>Vertical Moment (N-m):</td> <td><input id="input_my" tabindex="0" type="number"></td> </tr> <tr> <td>Horizontal Moment (N-m):</td> <td><input id="input_mr" tabindex="0" type="number"></td> </tr> <tr> <td>Adjustment Factor for Life Calc. (0.4 - 1):</td> <td><input id="input_af" tabindex="0" type="number" value="1"></td> </tr> </tbody> </table>

LoPro® RTU-L

Lf =
0
0
+
0
0
+
0
0
+
0
0
= 0



Life Estimate =
LC
(LF)3
*AF =
173
(0)3
*1.0 = 0 N

 

LoPro® RTU-M

Lf =
0
0
+
0
0
+
0
0
+
0
0
= 0



Life Estimate =
LC
(LF)3
*AF =
173
(0)3
*1.0 = 0 N

 

 

Example Robot Vertical Force (N) Horizontal Force (N) Vertical Moment (N-m) Horizontal Moment (N-m) Thrust (N) Recommended System(s)
1428 821 236 814 821 LoPro RTU-M, LoPro RTU-L
2205 566 255 2007 566 LoPro RTU-M*

 

*Forces and moments given are max normal operating conditions as provided by the robot manufacurer (E-Stop is not considered). These values are only for reference, and specific applications may have lower loading than these values; please tailor the values in each input field to match your application for more accurate results.

 

Example Robot Vertical Force (N) Horizontal Force (N) Vertical Moment (N-m) Horizontal Moment (N-m) Thrust (N) Recommended System(s)
2205 566 255 2007 566 Heavy Duty, LoProX2*
3386 715 549 3844 715 Heavy Duty
9248 3896 1582 7719 3896 Heavy Duty
1428 821 236 814 821 LoProX2, LoPro
3850 1850 855 1750 1850 Heavy Duty
5500 2000 550 3400 2000 Heavy Duty
4170 2330 1120 3360 2330 Heavy Duty
1475 2945 1275 1670 2945 Heavy Duty
7258 3434 2011 5150 3434 Heavy Duty
1043 715 549 3360 715 Heavy Duty

Thrust Calculation

Enter the max velocity of your application to see the thrust capabilities of the LoPro RTU belt drive:

<!---------VELOCITY CALCULAITON------------> <table> <tbody> <tr> <td>RTU Velocity for Thrust Calc. (m/s):</td> <td><input id="input_v" tabindex="0" type="number"></td> </tr> </tbody> </table> <div class="math-box"><!------start of math div---------> Max Thrust = 2818 - 4.80*V<sup>3</sup> + 60.0*V<sup>2</sup> - 369*V <br><span style="margin-left: 40px;"> = </span> 2818 - 4.80*<span class="velocity">0</span><sup>3</sup> + 60.0*<span class="velocity">0</span><sup>2</sup> - 369*<span class="velocity">0</span> = <span class="thrust_result" data-explain="true">2818 N</span> <!-----end of math div------></div> <p>(Max thrust for both light and medium RTUs is dependent on velocity.) <br><br></p>
<script type="text/javascript" language="javascript" charset="utf-8"> //LOAD CAPACITY DATA, block scoped //8 wheel, heavy duty const la_max_hd = 52416; const lr_max_hd = 57200; const my_max_hd = 14834; const mr_max_hd = 12648; const thrust_max_hd = 9948; //LP 2 plate const la_max_lpx2 = 31368; const lr_max_lpx2 = 38024; const my_max_lpx2 = 2956; const mr_max_lpx2 = 2348; const thrust_max_lpx2 = 2818; //LP 1 plate const la_max_lp = 15684; const lr_max_lp = 19012; const my_max_lp = 1478; const mr_max_lp = 1174; const thrust_max_lp = 2818; //set denominators const lp_la = document.querySelectorAll('[data-product="LP"][data-loadtype="la"]'); const lp_lr = document.querySelectorAll('[data-product="LP"][data-loadtype="lr"]'); const lp_my = document.querySelectorAll('[data-product="LP"][data-loadtype="my"]'); const lp_mr = document.querySelectorAll('[data-product="LP"][data-loadtype="mr"]'); const lpx2_la = document.querySelectorAll('[data-product="LPX2"][data-loadtype="la"]'); const lpx2_lr = document.querySelectorAll('[data-product="LPX2"][data-loadtype="lr"]'); const lpx2_my = document.querySelectorAll('[data-product="LPX2"][data-loadtype="my"]'); const lpx2_mr = document.querySelectorAll('[data-product="LPX2"][data-loadtype="mr"]'); for(var i = 0; i < lp_la.length; i++) {let current = lp_la[i]; current.innerHTML = la_max_lp;} for(var i = 0; i < lp_lr.length; i++) {let current = lp_lr[i]; current.innerHTML = lr_max_lp;} for(var i = 0; i < lp_my.length; i++) {let current = lp_my[i]; current.innerHTML = my_max_lp;} for(var i = 0; i < lp_mr.length; i++) {let current = lp_mr[i]; current.innerHTML = mr_max_lp;} for(var i = 0; i < lpx2_la.length; i++) {let current = lpx2_la[i]; current.innerHTML = la_max_lpx2;} for(var i = 0; i < lpx2_lr.length; i++) {let current = lpx2_lr[i]; current.innerHTML = lr_max_lpx2;} for(var i = 0; i < lpx2_my.length; i++) {let current = lpx2_my[i]; current.innerHTML = my_max_lpx2;} for(var i = 0; i < lpx2_mr.length; i++) {let current = lpx2_mr[i]; current.innerHTML = mr_max_lpx2;} //function to set numerators and perform calculations document.getElementById('input_la').addEventListener('input', lf_calc); document.getElementById('input_lr').addEventListener('input', lf_calc); document.getElementById('input_my').addEventListener('input', lf_calc); document.getElementById('input_mr').addEventListener('input', lf_calc); document.getElementById('input_af').addEventListener('input', lf_calc); function lf_calc(e){ let la = Math.abs(parseFloat(document.getElementById('input_la').value)) ||0; let lr = Math.abs(parseFloat(document.getElementById('input_lr').value)) ||0; let my = Math.abs(parseFloat(document.getElementById('input_my').value)) ||0; let mr = Math.abs(parseFloat(document.getElementById('input_mr').value)) ||0; let af = Math.abs(parseFloat(document.getElementById('input_af').value)) ||0; //display in formula const in_displays = document.getElementsByClassName('input_display'); const disp_la = document.querySelectorAll('[class="input_display"][data-loadtype="la"]'); const disp_lr = document.querySelectorAll('[class="input_display"][data-loadtype="lr"]'); const disp_my = document.querySelectorAll('[class="input_display"][data-loadtype="my"]'); const disp_mr = document.querySelectorAll('[class="input_display"][data-loadtype="mr"]'); const result_lp = document.querySelectorAll('[class="result_display"][data-product="LP"]'); const result_lpx2 = document.querySelectorAll('[class="result_display"][data-product="LPX2"]'); const disp_life_lp = document.querySelectorAll('[class="life_result"][data-product="LP"]'); const disp_life_lpx2 = document.querySelectorAll('[class="life_result"][data-product="LPX2"]'); const disp_af = document.querySelectorAll('[class="af_display"]'); for(var i = 0; i < disp_la.length; i++) {let current = disp_la[i]; current.innerHTML = la;} for(var i = 0; i < disp_lr.length; i++) {let current = disp_lr[i]; current.innerHTML = lr;} for(var i = 0; i < disp_my.length; i++) {let current = disp_my[i]; current.innerHTML = my;} for(var i = 0; i < disp_mr.length; i++) {let current = disp_mr[i]; current.innerHTML = mr;} //calc results let lp_pass = false; let lpx2_pass = false; let lf_calc_lp = la/la_max_lp + lr/lr_max_lp + my/my_max_lp + mr/mr_max_lp; let lf_disp_lp = Math.ceil(lf_calc_lp * 1000) / 1000; if(lf_calc_lp<1){lp_pass = true;} let life_calc_lp = 173*af/lf_disp_lp/lf_disp_lp/lf_disp_lp; // could use lf_calc, but this is more conservative let life_disp_lp = Math.ceil(life_calc_lp); let lf_calc_lpx2 = la/la_max_lpx2 + lr/lr_max_lpx2 + my/my_max_lpx2 + mr/mr_max_lpx2; let lf_disp_lpx2 = Math.ceil(lf_calc_lpx2 * 1000) / 1000; if(lf_calc_lpx2<1){lpx2_pass = true;} let life_calc_lpx2 = 173*af/lf_disp_lpx2/lf_disp_lpx2/lf_disp_lpx2; // could use lf_calc, but this is more conservative let life_disp_lpx2 = Math.ceil(life_calc_lpx2); for(var i = 0; i < result_lp.length; i++) { let current = result_lp[i]; current.innerHTML = lf_disp_lp; current.style = "color:black"; if (current.hasAttribute("data-explain")) { if (lp_pass) {current.innerHTML += " < 1; PASS";} else {current.innerHTML += " >= 1; Reduce Loads"; current.style = "color:red";} } } for(var i = 0; i < result_lpx2.length; i++) { let current = result_lpx2[i]; current.innerHTML = lf_disp_lpx2; current.style = "color:black"; if (current.hasAttribute("data-explain")) { if (lpx2_pass) {current.innerHTML += " < 1; PASS";} else {current.innerHTML += " >= 1; Reduce Loads"; current.style = "color:red";} } } for(var i = 0; i < disp_life_lp.length; i++) { let current = disp_life_lp[i]; current.innerHTML = life_disp_lp; current.style = "color:black"; if (current.hasAttribute("data-explain")) { if (lp_pass) {current.innerHTML += " km of travel";} else {current.innerHTML = "Reduce Loads"; current.style = "color:red";} } } for(var i = 0; i < disp_life_lpx2.length; i++) { let current = disp_life_lpx2[i]; current.innerHTML = life_disp_lpx2; current.style = "color:black"; if (current.hasAttribute("data-explain")) { if (lpx2_pass) {current.innerHTML += " km of travel";} else {current.innerHTML = "Reduce Loads"; current.style = "color:red";} } } for(var i = 0; i < disp_af.length; i++) { let current = disp_af[i]; current.innerHTML = af; } } </script>
<script type="text/javascript" language="javascript" charset="utf-8"> // THRUST CALCULATION BLOCK document.getElementById('input_v').addEventListener('input', thrust_calc); function thrust_calc(e) { let v = Math.abs(parseFloat(document.getElementById('input_v').value)) ||0; const disp_v = document.querySelectorAll('[class="velocity"]'); for(var i = 0; i < disp_v.length; i++) {let cur = disp_v[i]; cur.innerHTML = v;} // velocity-dependent thrust capacity for size 4 lopro let max_thrust = 2818 - 4.8*v*v*v + 60*v*v - 369*v; const disp_thrust = document.querySelectorAll('[class="thrust_result"]'); for(var i = 0; i < disp_thrust.length; i++) { let current = disp_thrust[i]; current.innerHTML = Math.ceil(max_thrust * 10000) / 10000; current.style = "color:black"; if (current.hasAttribute("data-explain")) { if (v>5.5) {current.innerHTML = "Velocity is too high for guide wheels. Maximum velocity is 5.5 m/s."; current.style = "color:red";} else if (max_thrust>0) {current.innerHTML += " N";} else {current.innerHTML = "Velocity is too high for belt shear strength."; current.style = "color:red";} } } } </script>
<script type="text/javascript" language="javascript" charset="utf-8"> //robot button press plugs values into input and runs calculations document.addEventListener('click', function(e){ if(e.target.className=="roboButton"){ let dataC = e.target.closest('tr').children; document.getElementById('input_la').value = dataC[1].textContent; document.getElementById('input_lr').value = dataC[2].textContent; document.getElementById('input_my').value = dataC[3].textContent; document.getElementById('input_mr').value = dataC[4].textContent; } lf_calc(); }) </script>
Product Details
  • Product Info
  • Specification
  • Success Stories
  • Faqs
  • Reviews

Add extremely durable 7th axes and robot transfer units (RTUs) for your favorite robot brands

Support and transfer robot arms of any size with Bishop-Wisecarver’s suite of robot transfer solutions. We provide reliable, long-lasting RTUs and 7th axis systems for all your favorite brands of cobots and industrial arms.

Our expertly designed robot transfer systems excel in even the harshest environments and most extreme applications. Each system is built on DualVee Motion Technology® for self-cleaning guidance, low maintenance, and unparalleled dependability.

Many solutions that run on DualVee guide wheels require no maintenance over the planned life of the machine. This ability to excel in critical applications makes Bishop-Wisecarver's solutions ideal for drilling, welding, painting, and more.

LoPro RTU-L and LoPro RTU-M

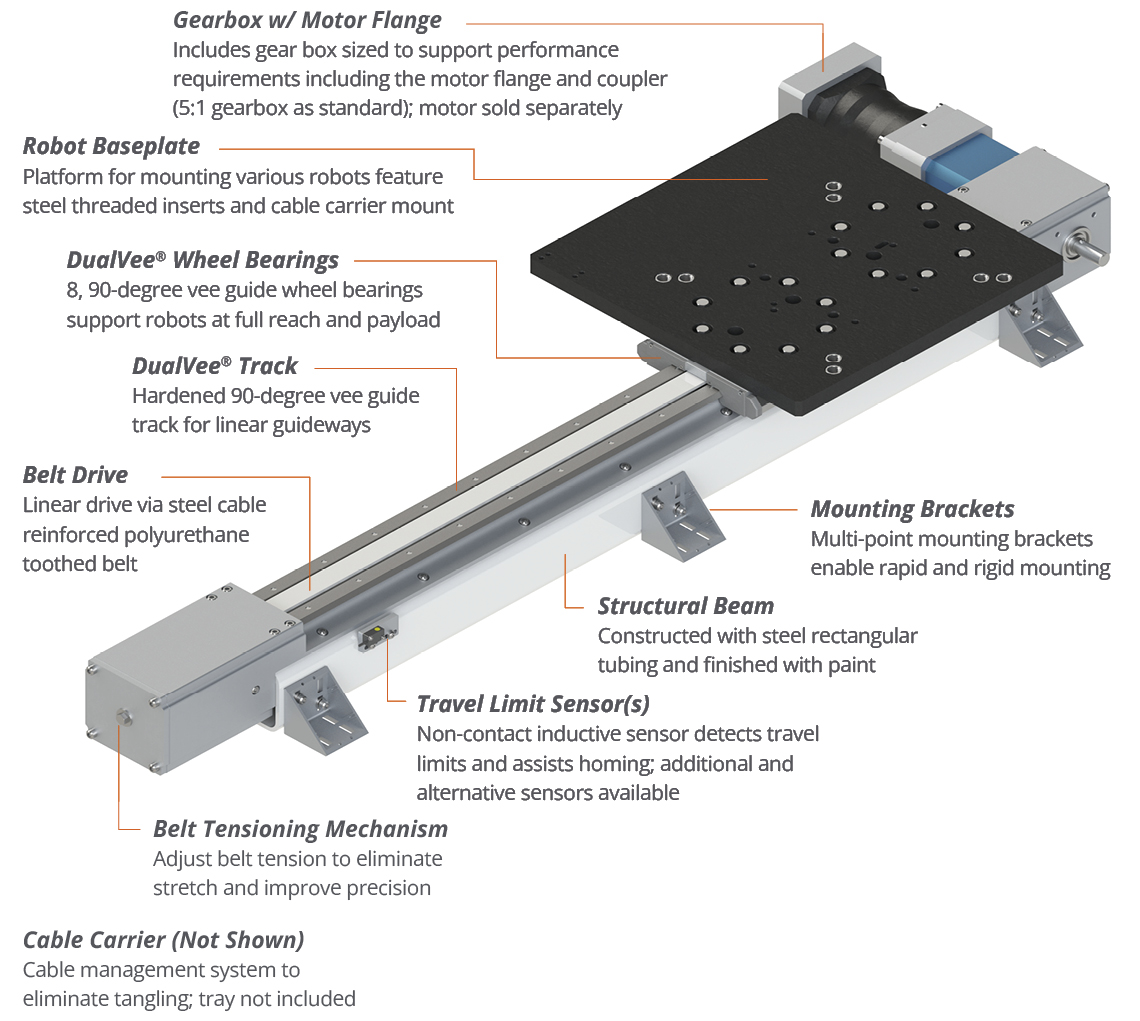
LoPro 7th axis features

 

Includes:

  • Belt-driven actuator with single wheel plate (RTU-L) or double wheel plate (RTU-M)
  • Mounting plate with hole pattern matched to your robot
  • 5:1 planetary gearbox as standard
  • Motor mount matched to your drive motor of choice
  • Cable carrier
  • Home and limit switches

Simply provide the robot, drive motor, and cabling!

 

Standard Features:

  • Debris-resistant and extremely durable DualVee wheels
  • Ready-to-mount bracketing assembled on a rigid steel base
  • Belt tensioning and wheel adjustment systems designed for easy maintenance
  • Painted base and anodized plates/brackets

 

 

Need customization? Talk to us!

  • Removing included elements
  • Alternate gearbox
  • Alternate limit switch configuration
  • Cable carrier with pre-installed cables
  • Additional drive shaft (opposite the motor mounting side, for coupling etc.)
  • Custom lengths
  • Additional machining or alternate finishing

Stock Codes

LoPro RTU stock code system

System Capabilities

 

Vertical Force
(LA)

Horizontal Force
(LR)

Vertical Moment
(MY)

Horizontal Moment
(MR)

Horizontal Moment
(MP)

Thrust
(Approximate, Slow Speed)
  N N N-m N-m N-m N

LoPro RTU-L
(Light Capacity, Single Wheel Plate)

 15684 19012 1478 1174 1220 2818

LoPro RTU-M
(Medium Capacity,  Double Wheel Plate)

 31368 38024 2956 2348 2440 2818

 

 

Load & Life Calculation

The following equation is for the purpose of estimating the applied load factor to the wheel plate and track plate only. System drive components are not accounted for, but should also be considered. The expected life of the system (in travel length, such as inches or kilometers) is calculated using:

Life =
LC
(LF)3
*AF

 

 

The Life Constant (Lc) is given in the table on the right.

The Adjustment Factor (Lf) is estimated based on the severity of application conditions (see table on the right).

The Load Factor (Lf) is calculated using the application's applied forces/moments and force/moment capacities of the system as follows:

Lf =
Fvertical
LA(max)
+
Fhorizontal
LR(max)
+
Mvertical
MY(max)
+
Mhorizontal
MR(max)

 

 

Refer to the illustration on the right for directions of each component. Any forces applied on the wheel plate need to be considered, including inertial forces, gravitational forces, external forces such as tool pressure, impact loading, and payload.

The most conservative calculations will use max foundational loading values from robot manufacturer catalogs. Note that since the robot can only be extended in one horizontal direction, pitch moment (MP) found in other LoPro actuator-based system calculations is ignored.

If assistance is required in resolving specific loads into the resultant forces, please contact our Applications Engineering staff.

 

 

 

 

load orientation diagram

 

life constant and adjustment factor charts

Enter the necessary mounting capacities of your robot, or select an example robot from the list below:

Vertical Force (N):
Horizontal Force (N):
Vertical Moment (N-m):
Horizontal Moment (N-m):
Adjustment Factor for Life Calc. (0.4 - 1):

LoPro® RTU-L

Lf =
0
0
+
0
0
+
0
0
+
0
0
= 0



Life Estimate =
LC
(LF)3
*AF =
173
(0)3
*1.0 = 0 N

 

LoPro® RTU-M

Lf =
0
0
+
0
0
+
0
0
+
0
0
= 0



Life Estimate =
LC
(LF)3
*AF =
173
(0)3
*1.0 = 0 N

 

 

Example Robot Vertical Force (N) Horizontal Force (N) Vertical Moment (N-m) Horizontal Moment (N-m) Thrust (N) Recommended System(s)
1428 821 236 814 821 LoPro RTU-M, LoPro RTU-L
2205 566 255 2007 566 LoPro RTU-M*

 

*Forces and moments given are max normal operating conditions as provided by the robot manufacurer (E-Stop is not considered). These values are only for reference, and specific applications may have lower loading than these values; please tailor the values in each input field to match your application for more accurate results.

 

Example Robot Vertical Force (N) Horizontal Force (N) Vertical Moment (N-m) Horizontal Moment (N-m) Thrust (N) Recommended System(s)
2205 566 255 2007 566 Heavy Duty, LoProX2*
3386 715 549 3844 715 Heavy Duty
9248 3896 1582 7719 3896 Heavy Duty
1428 821 236 814 821 LoProX2, LoPro
3850 1850 855 1750 1850 Heavy Duty
5500 2000 550 3400 2000 Heavy Duty
4170 2330 1120 3360 2330 Heavy Duty
1475 2945 1275 1670 2945 Heavy Duty
7258 3434 2011 5150 3434 Heavy Duty
1043 715 549 3360 715 Heavy Duty

Thrust Calculation

Enter the max velocity of your application to see the thrust capabilities of the LoPro RTU belt drive:

RTU Velocity for Thrust Calc. (m/s):
Max Thrust = 2818 - 4.80*V3 + 60.0*V2 - 369*V
= 2818 - 4.80*03 + 60.0*02 - 369*0 = 2818 N

(Max thrust for both light and medium RTUs is dependent on velocity.)

LoPro 7th Axis Gray Matter

7TH AXIS FOR ROBOTIC SANDING

Durable and Easy-to-Implement Robot Transfer Solution

THE CHALLENGE:

GrayMatter’s Scan&Sand™ system needed to consistently
produce superior results while sanding variable workpieces. This robot transfer unit supports their self-programming algorithms; it must be easy to set up, operate, and maintain. Abrasive debris and factory dust cannot stand in the way.

INDUSTRY: Manufacturing - Robotics

PRODUCT USED: LoPro 7th Axis

What is a Robot Transfer Unit?

Robot positioning systems (7th axis or Robot Transfer Units) provide flexibility in manufacturing and industrial spaces. For example, they may allow one robot to reposition between work stations to do the work of several robots. They may also extend a robot’s working area without need for a larger arm. Sometimes, the transfer of units away from the operating zone permits safe movement of workers or large equipment.

These motion systems are common in aerospace, automotive, warehouse, and manufacturing applications. Both traditional and collaborative robots can benefit from Bishop-Wisecarver’s 7th axis motion solutions, regardless of their size.

Why Bishop-Wisecarver?

Bishop-Wisecarver specializes in motion solutions that are expertly designed and delivered to perform, from a company you can trust.

Our solutions deliver maximum environmental and debris resistance. This ability to excel in harsh and extreme conditions is especially critical for drilling, welding, painting, etc.

Additionally, BW systems are specifically design by our motion experts to minimize your installation effort and maintenance costs. Many solutions require no maintenance over the planned life of the machine. (Click here to read more about the total cost of ownership advantage of our products.)

We don’t just deliver quality products; we deliver a Signature Experience™ to our customers. Bishop-Wisecarver’s expert application engineers can help you select the complete 7th axis system solution that is right for you, including motors and controls. Our team can also partner with you to design a fully customized system that meets your application requirements.

Write Your Own Review

Only registered users can write reviews. Please Sign in or create an account
Contact
Subscribe to the Pioneering Edge newsletter to stay on top of the rapidly changing technologies that can impact your business.
© 2023 - Bishop-Wisecarver